АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ И МИНОРЫ

Пусть имеем определитель третьего порядка: .

Минором , соответствующим данному элементу a ij определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i -ой строки и j -го столбца. Миноры соответствующие данному элементу a ij будем обозначать M ij .

Например , минором M 12 , соответствующим элементу a 12 , будет определитель , который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.

Таким образом, формула, определяющая определитель третьего порядка, показывает, что этот определитель равен сумме произведений элементов 1-ой строки на соответствующие им миноры; при этом минор, соответствующий элементу a 12 , берётся со знаком “–”, т.е. можно записать, что

.

(1)

Аналогично можно ввести определения миноров для определителей второго порядка и высших порядков.

Введём ещё одно понятие.

Алгебраическим дополнением элемента a ij определителя называется его минор M ij , умноженный на (–1) i+j .

Алгебраическое дополнение элемента a ij обозначается A ij .

Из определения получаем, что связь между алгебраическим дополнением элемента и его минором выражается равенством A ij = (–1) i+j M ij .

Например,

Пример. Дан определитель . Найти A 13 , A 21 , A 32 .

Легко видеть, что используя алгебраические дополнения элементов, формулу (1) можно записать в виде:

Аналогично этой формуле можно получить разложение определителя по элементам любой строки или столбца.

Например, разложение определителя по элементам 2-ой строки можно получить следующим образом. Согласно свойству 2 определителя имеем:

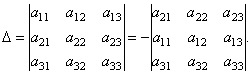
Разложим полученный определитель по элементам 1-ой строки.

.

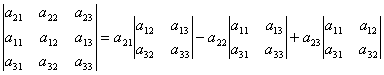(2)

Отсюда т.к. определители второго порядка в формуле (2) есть миноры элементов a 21 , a 22 , a 23 . Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой строки.

Аналогично можно получить разложение определителя по элементам третьей строки. Используя свойство 1 определителей (о транспонировании), можно показать, что аналогичные разложения справедливы и при разложении по элементам столбцов.

Таким образом, справедлива следующая теорема.

Теорема (о разложении определителя по заданной строке или столбцу). Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения.

Всё вышесказанное справедливо и для определителей любого более высокого порядка.

Примеры.

ОБРАТНАЯ МАТРИЦА

Понятие обратной матрицы вводится только для квадратных матриц .

Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A -1 и удовлетворяющая условию . (Это определение вводится по аналогии с умножением чисел)

Квадратной матрице А порядка n можно сопоставить число det А (или |A |, или ), называемое ее определителем , следующим образом:

Определитель матрицы A также называют ее детерминантом . Правило вычисления детерминанта для матрицы порядка N является довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда (свойство 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению.

Вычисление определителя 2-го порядка иллюстрируется схемой:

Пример 4.1. Найти определители матриц

При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:

Пример 4.2. Вычислить определитель матрицы

det А = 5*1*(-3) + (-2)*(-4)*6 + 3*0*1 — 6*1*1 — 3*(-2)*(-3) — 0*(-4)*5 = -15+48-6-18 = 48-39 = 9.

Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.

Свойство 1 («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот. Иными словами,

В дальнейшем строки и столбцы будем просто называть рядами определителя .

Свойство 2 . При перестановке двух параллельных рядов определитель меняет знак.

Свойство 3 . Определитель, имеющий два одинаковых ряда, равен нулю.

Свойство 4 . Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.

Действительно,

Свойство 5 . Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

Например,

Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одною ряда прибавить соответствующие элементы параллельного ряда, умноженные па любое число.

Пример 4.3 . Доказать, что

Решение: Действительно, используя свойства 5, 4 и 3 подучим

Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.

Минором некоторого элемента аij определителя n- го порядка называется определитель n — 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, па пересечении которых находится выбранный элемент. Обозначается mij

Алгебраическим дополнением элемента aij определителя называется его минор, взятый со знаком «плюс», если сумма i + j четное число, и со знаком «минус», если эта сумма нечетная. Обозначается Aij :

Свойство 7 («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.

Она поможет не только чайникам, но даже тем, кто впервые услышал слово «определитель». Минуло два года с тех пор, когда на сайте было всего десять страничек, и вот, после моего долгого-долгого путешествия в мир матана, всё возвращается на круги своя.

Представьте, что вам нужно вычислить определитель третьего порядка, разложив его по элементам строки (столбца). Хотя чего тут представлять – нужно же =) Над ним можно сидеть 5 минут, а можно 2-3 минуты. Или даже в районе одной минуты. Время, которое вы потратите, зависит не только от вашего опыта, но и от знаний свойств определителей. Не редкость, когда процесс решения вполне реально сократить до считанных секунд, а иногда и сразу увидеть результат! «Ерунда, чего экономить на спичках, и так всё решим», – скажут некоторые. Допустим. И не допустим оплошностей;-) Но как быть с достаточно распространённым на практике определителем 4-го порядка? Воевать с этим перцем придётся уже 10-20 минут. И это будет даже не бой, а бойня, поскольку очень велика вероятность вычислительной ошибки, которая «завернёт» вас на второй круг решения. А если определитель пятого порядка? Спасёт только понижение порядка определителя. Да, такие примеры тоже встречаются в контрольных работах.

Материалы данной страницы позволят значительно улучшить вашу технику решения определителей и упростят дальнейшее освоение высшей математики.

Эффективные методы вычисления определителя

В первую очередь коснёмся не свойств определителя, а как раз методов его рационального вычисления. Эти приёмы решения лежат на поверхности и понятны многим, но всё-таки остановимся на них подробнее. Предполагается, что читатель уже умеет достаточно уверенно раскрывать определитель третьего порядка. Как известно, данный определитель можно раскрыть 6 стандартными способами: по любой строке или любому столбцу. Казалось бы, без разницы, ведь ответ получится один и тот же. Но все ли способы одинаково легкИ? Нет. В большинстве случаев есть менее выгодные пути и более выгодные пути решения.

Рассмотрим определитель , который я обильно покрыл татуировками ещё на первом уроке. В той статье мы подробно, с картинками разложили его по первой строке. Первая строка – это хорошо и академично, однако нельзя ли быстрее достичь результата? В определителе есть ноль, и, раскрывая его по второй строке либо по второму столбцу, вычислений заметно поубавится!

Разложим определитель по второму столбцу:

На практике нулевые элементы игнорируются, и запись решения принимает более компактный вид:

Задание 1

Раскройте данный определитель по второй строке, используя укороченную запись.

Решение в конце урока.

Если в строке (либо столбце) два нуля, то это вообще настоящий подарок. Рассмотрим определитель . Здесь два нуля в третьей строке, по ней и раскрываем:

Вот и всё решение!

Особый случай, когда определитель имеет так называемый ступенчатый или треугольный вид , например: – в таком определителе все числа, расположенные ниже главной диагонали , равны нулю.

Разложим его по первому столбцу:

В практических заданиях удобно руководствоваться следующим правилом – ступенчатый определитель равен произведению чисел его главной диагонали :

Аналогичный принцип справедлив и для ступенчатых определителей других порядков, например:

Треугольные определители появляются в некоторых задачах линейной алгебры, и их решение чаще всего оформляют именно так.

А если в строке (столбце) определителя находятся одни нули ? Ответ, думаю, понятен. Мы ещё вернёмся к этому вопросу в свойствах определителя.

Теперь представим, что долгожданные баранки не положены в новогодний подарок. Так давайте же распотрошим нехорошего Санта-Клауса!

Здесь нет нулей, но всё равно существует способ облегчить себе жизнь. Данный определитель оптимальнее разложить по третьему столбцу, поскольку там самые маленькие числа. При этом запись решения принимает весьма лаконичный вид:

Резюмируя параграф, сформулируем золотое правило вычислений:

Определитель выгоднее раскрывать по ТОЙ строке (столбцу), где:

1) нулей побольше ;
2) числа поменьше .

Естественно, это справедливо и для определителей высших порядков.

Небольшой пример для закрепления материала:

Задание 2

Вычислить определитель, раскрыв его по строке либо столбцу, используя при этом наиболее рациональный способ

Это пример для самостоятельного решения, оптимальное решение и ответ – в конце урока.

И ещё один важный совет: не комплексуйте! Не нужно «зацикливаться» на традиционном разложении по первой строке либо первому столбцу. Как короче – так и решайте!

Свойства определителя

Рассмотрим старых знакомых первого урока: матрицу и её определитель .

На всякий случай повторю элементарное различие между понятиями: матрица – это таблица элементов , а определитель – это число .

При транспонировании матрицы величина её определителя не меняется

Транспонируем матрицу:

Согласно свойству, определитель транспонированной матрицы равен тому же значению: . Желающие могут убедиться в этом самостоятельно.

В ходу и более простецкая формулировка данного свойства: если транспонировать определитель, то его величина не изменится.

Запишем оба определителя рядышком и проанализируем один важный момент:

В результате транспонирования первая строка стала первым столбцом, вторая строка – вторым столбцом, третья строка – третьим столбцом. Строки стали столбцами, а результат не изменился. Из чего следует важный факт: строки и столбцы определителя равноправны . Иными словами, если какое-нибудь свойство справедливо для строки, то аналогичное свойство справедливо и для столбца! В действительности с этим мы уже давно столкнулись – ведь определитель можно раскрыть как по строке, так равноправно и по столбцу.

Не нравятся числа в строках? Транспонируйте определитель! Возникает только один вопрос, зачем? Практический смысл рассмотренного свойства невелик, но его полезно закинуть в багаж знаний, чтобы лучше понимать другие задачи высшей математики. Например, сразу становится ясно, почему при исследовании векторов на компланарность их координаты можно записать как в строки определителя, так и в столбцы.

Если две строки (или два столбца) определителя поменять местами,
то определитель сменит знак

! Помните , речь идёт об определителе! В самой матрице переставлять ничего нельзя!

Сыграем в кубик-рубик с определителем .

Поменяем первую и третью строку местами:

Определитель сменил знак.

Теперь в полученном определителе переставим вторую и третью строки:

Определитель ещё раз изменил знак.

Переставим второй и третий столбец:

То есть, любая парная перестановка строк (столбцов) влечёт изменение знака определителя на противоположный .

Игры играми, но на практике такие действия лучше не использовать . Толку от них особого нет, а вот запутаться и допустить ошибку несложно. Однако приведу одну из немногих ситуаций, когда в этом действительно есть смысл. Предположим, что в ходе решения некоторого примера у вас нарисовался определитель со знаком «минус»:

Раскроем его, скажем, по первой строке:

Очевидное неудобство состоит в том, что пришлось выполнять лишние реверансы – ставить большие скобки, а затем их раскрывать (кстати, крайне не рекомендую выполнять подобные действия «за один присест» устно).

Чтобы избавиться от «минуса», рациональнее поменять местами любые две строки или любые два столбца. Переставим, например, первую и вторую строки:

Выглядит стильно, но в большинстве случаев с отрицательным знаком целесообразнее разбираться другим способом (читайте дальше).

Рассмотренное действие опять же помогает лучше понять, например, некоторые свойства векторного произведения векторов или смешанного произведения векторов.

А вот это уже более интересно:

Из строки (столбца) определителя можно вынести общий множитель

!!! Внимание! В правиле речь идёт об ОДНОЙ строке или об ОДНОМ столбце определителя. Пожалуйста, не путайте с матрицами , в матрице множитель выносится/вносится у ВСЕХ чисел сразу.

Начнём с частного случая правила – вынесения «минус единицы» или просто «минуса».

Встречаем очередного пациента: .

В данном определителе слишком много минусов и неплохо бы сократить их количество.

Вынесем –1 из первой строки:

Или короче:

Минус перед определителем, как уже демонстрировалось – не есть удобно. Смотрим на вторую строку определителя и замечаем, что минусов там тоже многовато.

Вынесем «минус» из второй строки:

Что можно сделать ещё? Все числа второго столбца делятся на 4 без остатка. Вынесем 4 из второго столбца:

Справедливо и обратное правило – множитель можно не только вынести, но и внести , причём, в ЛЮБУЮ строку или в ЛЮБОЙ столбец определителя.

Ради шутки умножим на 4 третью строку определителя:

Дотошные умы могут убедиться в равенстве исходного и полученного определителей (верный ответ: –216).

На практике часто выполняют внесение минуса. Рассмотрим определитель . Отрицательный знак перед определителем можно внести в ЛЮБУЮ строку или в ЛЮБОЙ столбец. Самым лучшим кандидатом является третий столбец, в него и внесём минус:

Также замечаем, что все числа первого столбца делятся на 2 без остатка, но стОит ли выносить «двойку»? Если вы собираетесь понижать порядок определителя (о чём пойдет речь в заключительном разделе), то, безусловно, стОит. Но если раскрывать определитель по строке (столбцу), то «двойка» впереди только удлинит запись решения.

Однако если множитель велик, например, 13, 17 и т.п., то его, конечно, по-любому выгоднее вынести. Познакомимся с маленьким монстром: . Из первой строки вынесем –11, из второй строки вынесем –7:

Вы скажете, вычисления и так быстро щёлкаются на обычном калькуляторе? Это правда. Но, во-первых, его может не оказаться под рукой, а во-вторых, если дан определитель 3-го или 4-го порядка с большими числами, то и стучать по кнопкам уже не сильно захочется.

Задание 3

Вычислить определитель с помощью вынесения множителей из строк и столбцов

Это пример для самостоятельного решения.

Ещё пара полезных правил:

Если две строки (столбца) определителя пропорциональны
(как частный случай – одинаковы), то данный определитель равен нулю

Здесь пропорциональны соответствующие элементы первой и второй строки:

Иногда говорят, что строки определителя линейно зависимы . Так как при транспонировании величина определителя не меняется, то из линейной зависимости строк следует и линейная зависимость столбцов.

В пример можно вложить геометрический смысл – если считать, что в строках записаны координаты векторов пространства, то первые два вектора с пропорциональными координатами будут коллинеарны, а значит, все три вектора – линейно зависимы , то есть компланарны.

В следующем примере пропорциональны три столбца (и, к слову, три строки тоже):

Здесь второй и третий столбец одинаковы, это частный случай – когда коэффициент пропорциональности равен единице

Перечисленные свойства вполне можно использовать на практике. Но помните, повышенный уровень знаний иногда наказуем;-) Поэтому, возможно, лучше раскрывать такие определители обычным способом (зная наперёд, что получится ноль).

Следует отметить, что обратное в общем случае неверно – если определитель равен нулю, то из этого ещё не следует , что его строки (столбцы) пропорциональны. То есть линейная зависимость строк/столбцов может быть и не явной.

Существуют и более очевидный признак, когда сразу можно сказать, что определитель нулевой:

Определитель с нулевой строкой (столбцом) равен нулю

«Любительская» проверка элементарна, раскроем определитель по первому столбцу:

Впрочем, результат не изменится, если раскрыть определитель по любой строке или любому столбцу.

Выжимаем второй стакан апельсинового сока:

Какие свойства определителей полезно знать?

1) Величина определителя не меняется при транспонировании . Свойство запоминаем.

2) Любая парная перестановка строк (столбцов) меняет знак определителя на противоположный . Свойство тоже запоминаем и стараемся не использовать во избежание путаницы.

3) Из строки (столбца) определителя можно вынести множитель (и внести его обратно) . Используем там, где это выгодно.

4) Если строки (столбцы) определителя пропорциональны, то он равен нулю. Определитель с нулевой строкой (столбцом) равен нулю.

На протяжении урока неоднократно наблюдалась элементарная закономерность – чем больше в строке (столбце) нулей, тем легче вычислить определитель. Возникает вопрос, а нельзя ли нули организовать специально с помощью какого-нибудь преобразования? Можно! Познакомимся ещё с одним очень мощным свойством:

Понижение порядка определителя

Очень хорошо, если вы уже разобрались с методом Гаусса и имеете опыт решения систем линейных уравнений этим способом. Фактически сформулированное ниже свойство дублирует одно из элементарных преобразований .

Чтобы нагулять аппетит раздавим маленького лягушонка:

К строке определителя можно прибавить другую строку, умноженную на ненулевое число. При этом величина определителя не изменится

Пример: в определителе получим ноль слева вверху.

Для этого вторую строку мысленно либо на черновике умножим на 3: (–3, 6) и к первой строке прибавим вторую строку, умноженную на 3 :

Результат записываем в первую строку :

Проверка:

Теперь в том же определителе получим ноль справа внизу. Для этого ко второй строке прибавим первую строку, умноженную (мысленно) на –2 ):

Результат записываем во вторую строку :

Обратите внимание : при элементарном преобразовании меняется ТА строка, к которой прибавляЮТ .

Сформулируем зеркальное правило для столбцов:

К столбцу определителя можно прибавить другой столбец, умноженный на ненулевое число. При этом величина определителя не изменится

Возьмём за лапки животное и, используя данное преобразование, получим ноль слева вверху. Для этого мысленно либо на черновике умножим второй столбец на –3: и к первому столбцу прибавим второй столбец, умноженный на –3 :

Результат запишем в первый столбец :

И, наконец, в определителе получим ноль справа внизу. Для этого ко второму столбцу прибавим первый столбец, умноженный (мысленно) на 2 (смотрим и считаем справа налево ):

Результат помещаем во второй столбец :

При элементарном преобразовании меняется ТОТ столбец, к которому прибавляЮТ .

Постарайтесь качественно переварить нижеследующий пример.

Отправим в суп подросшее земноводное:

Задача состоит в том, чтобы с помощью элементарных преобразований понизить порядок определителя до второго порядка.

С чего начать? Сначала в определителе нужно выбрать число-«мишень». В качестве «мишени» почти всегда выступает единица либо –1. Смотрим на определитель и замечаем, что здесь даже выбор есть. Пусть числом-«мишенью» будет элемент :

Примечание : смысл двойных подстрочных индексов можно узнать в статье Правило Крамера. Матричный метод . В данном случае индексы элемента говорят нам о том, что он располагается во второй строке, третьем столбце.

Идея состоит в том, чтобы получить два нуля в третьем столбце:

Либо получить два нуля во второй строке:

Во второй строке числа поменьше (не забываем золотое правило), поэтому выгоднее взять именно её. А третий столбец с числом-«мишенью» останется неизменным:

Ко второму столбцу прибавляем третий столбец :

Тут и умножать ничего не пришлось.

Результат записываем во второй столбец:

К первому столбцу прибавляем третий столбец, умноженный (мысленно) на –2 :

Результат записываем в первый столбец, раскладываем определитель по второй строке:

Как мы понизили порядок определителя? Получили два нуля во второй строке.

Решим пример вторым способом, организуем нули в третьем столбце:

Вторая строка с числом-«мишенью» останется неизменной:

К первой строке прибавим вторую строку, умноженную (мысленно) на –4:

К третьей строке прибавим вторую строку, умноженную (мысленно) на 3 (смотрим и считаем снизу вверх) :

Результат записываем в третью строку, определитель раскрываем по третьему столбцу:

Заметьте, что нет никакой необходимости переставлять строки или столбцы . Элементарные преобразования прекрасно работают как слева направо, так и справа налево. Как сверху вниз, так и снизу вверх.

Задание 4

Вычислить тот же определитель , выбрав в качестве числа-«мишени» элемент . Понизить его порядок двумя способами: получив нули во второй строке и получив нули во втором столбце.

Это пример для самостоятельного решения. Полное решение и краткие комментарии в конце урока.

Иногда в определителе отсутствует единица либо –1, например: . В этом случае «мишень» следует организовать с помощью дополнительного элементарного преобразования. Сделать это можно чаще всего несколькими способами. Например: к первой строке прибавим вторую строку, умноженную –1:

Результат записываем в первую строку:

! Внимание : НЕ НУЖНО из первой строки вычитать вторую строку, это значительно увеличивает вероятность ошибки. Только складываем! Поэтому к первой строке прибавляем вторую строку, умноженную –1. Именно так!

Единица получена, чего и требовалось достичь. Далее можно получить два нуля в первой строке либо в первом столбце. Желающие могут довести решение до конца (верный ответ: –176).

Стоит отметить, что готовая «мишень» чаще всего присутствует в исходном определителе, а уж для определителя 4-го порядка и выше дополнительное преобразование крайне маловероятно.

Порубим на гуляш несколько крупных жаб:

Задача

Решить систему линейных уравнений по формулам Крамера

Ничего страшного, если вы ещё не успели ознакомиться с методом Крамера , в этом случае можно просто посмотреть, как понижается порядок у определителя «четыре на четыре». Да и само правило станет понятно, если чуть-чуть вникнуть в ход решения.

Решение : сначала вычислим главный определитель системы:

Есть возможность пойти стандартным путём, разложив данный определитель по строке либо столбцу. Вспоминая алгоритм первого урока, и, используя придуманную мной матрицу знаков , раскроем определитель, например, по «классической» первой строке:

Не вижу вашего энтузиазма =) Безусловно, можно посидеть минут десять и аккуратно-внимательно родить правильный ответ. Но беда в том, что в дальнейшем предстоит вычислить ещё 4 определителя четвёртого порядка. Поэтому единственный разумный выход – понизить порядок определителя.

Единиц в определителе много, и наша задача выбрать лучший вариант. Вспоминаем золотое правило: в строке (столбце) нулей должно быть побольше, и числа – поменьше. По этой причине вполне подходит вторая строка либо четвёртый столбец. Четвёртый столбец выглядит привлекательнее, причём, там есть две единицы. В качестве «мишени» выбираем элемент :

Первая строка не изменится. И вторая тоже – там уже необходимый ноль:

К третьей строке прибавим первую строку, умноженную на –1 (смотрим и считаем снизу вверх ):

! Внимание ещё раз : Не нужно из третьей строки вычитать первую строку. Только складываем!

Результат записываем в третью строку:

К четвёртой строке прибавим первую строку, умноженную на 3 (смотрим и считаем снизу вверх ):

Результат записываем в четвёртую строку:

(1) Раскрываем определитель по четвёртому столбцу. Не забываем, что к элементу нужно добавить «минус» (см. матрицу знаков).

(2) Порядок определителя понижен до 3-го. В принципе, его можно разложить по строке (столбцу), но лучше отработаем свойства определителя. Вносим минус во вторую строку.

(3) Ко второй строке прибавим первую строку, умноженную на 3. К третьей строке прибавим первую строку, умноженную на 7.

(4) Раскрываем определитель по второму столбцу, тем самым ещё понижая его порядок до двух.

Заметьте, как сократилось решение! Главное, немного «набить руку» на элементарных преобразованиях, и такая возможность представится прямо сейчас. К тому же в вашем распоряжении есть калькулятор, который считает определители (в частности, его можно найти на странице Математические формулы и таблицы ). С помощью калькулятора легко контролировать выполняемые действия. Получили определитель на первом шаге – и сразу проверили, равен ли он исходному определителю.

(1) Раскрываем определитель по третьей строке. Порядок определителя понижен до трёх.

(2) Вносим «минус» в первый столбец.

(3) Ко второй строке прибавим первую строку, умноженную на 3. К третьей строке прибавим первую строку, умноженную на 5.

(4) Раскрываем определитель по второму столбцу, понижая порядок определителя до двух.

Замечательный получается у нас комплексный обед, и пришло время десерта:

Это уже даже не жаба, это сам Годзилла. Возьмём заготовленный стакан апельсинового сока и посмотрим, как понижается порядок определителя. Алгоритм, думаю, понятен: с пятого порядка понижаем до четвёртого, с четвёртого – до третьего и с третьего – до второго:

(1) К первой, третьей, четвертой и пятой строкам прибавим вторую строку.

(2) Раскрываем определитель по 3-му столбцу. Порядок определителя понизился до четырёх.

(3) Из 4-го столбца выносим 2. Первую строку умножаем на –1, и чтобы определитель не изменился, ставим перед ним «минус». Данное преобразование выполнено в целях упростить дальнейшие вычисления.

(4) Ко второй и третьей строкам прибавим первую строку. К четвертой строке прибавим первую строку, умноженную на 3.

(5) Раскрываем определитель по 4-му столбцу. Порядок понижен до трёх.

(6) Раскрываем определитель по 2-му столбцу. Порядок понижен до двух.

(7) Выносим «минус» из 1-го столбца.

Всё вышло проще, чем казалось, у всех монстров есть слабые места!

Неутомимые читатели могут попробовать решить определитель пятого порядка каким-нибудь другим способом, благо, единиц в нём тьма.

К первому столбцу прибавили второй столбец, умноженный на 2. К третьему столбцу прибавили второй столбец. Определитель раскрыли по второй строке.

Понизим порядок определителя, получив нули во втором столбце:

К первой строке прибавили вторую строку, умноженную на –2. К третьей строке прибавили вторую строку, умноженную на 2. Определитель раскрыли по второму столбцу.

Задание 5: Решение :


(1) К первой строке прибавим третью строку, умноженную на 3. Ко второй строке прибавим третью строку, умноженную на 5. К 4-й строке прибавим третью строку, умноженную на 2.
(2) Раскрываем определитель по первому столбцу.
(3) Ко второму столбцу прибавим третий столбец, умноженный на 9. К первому столбцу прибавим третий столбец.
(4) Раскрываем определитель по третьей строке.

(1) К первому столбцу прибавим второй столбец. К третьему столбцу прибавим второй столбец
(2) Раскрываем определитель по третьей строке.
(3) Вносим «минус» в первую строку.
(4) Ко второй строке прибавим первую строку, умноженную на 6. К третьей строке прибавим первую строку
(5) Раскрываем определитель по первому столбцу.

Здесь будут изложены те свойства, которые обычно используются для вычисления определителей в стандартном курсе высшей математики. Это вспомогательная тема, к которой будем обращаться из остальных разделов по мере необходимости.

Итак, пусть задана некая квадратная матрица $A_{n\times n}=\left(\begin{array} {cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \\ \end{array} \right)$. Каждая квадратная матрица обладает характеристикой, которая называется определителем (или детерминантом). Я не стану вдаваться здесь в суть этого понятия. Если оно требует пояснений, то прошу отписать об этом на форум , и я коснусь данного вопроса детальнее.

Обозначается определитель матрицы $A$ как $\Delta A$, $|A|$ или $\det A$. Порядок определителя равен количеству строк (столбцов) в нём.

1. Значение определителя не изменится, если его строки заменить соответствующими столбцами, т.е. $\Delta A=\Delta A^T$.

   показать\скрыть

   Заменим в нём строки столбцами по принципу: "была первая строка - стал первый столбец", "была вторая строка - стал второй столбец":

   Вычислим полученный определитель: $\left| \begin{array} {cc} 2 & 9 \\ 5 & 4 \end{array} \right|=2\cdot 4-9\cdot 5=-37$. Как видите, значение определителя от проведённой замены не изменилось.

2. Если поменять местами две строки (столбца) определителя, то знак определителя изменится на противоположный.

   Пример применения этого свойства: показать\скрыть

   Рассмотрим определитель $\left| \begin{array} {cc} 2 & 5 \\ 9 & 4 \end{array} \right|$. Найдём его значение, используя формулу №1 из темы вычисления определителей второго и третьего порядков :

   $$\left| \begin{array} {cc} 2 & 5 \\ 9 & 4 \end{array} \right|=2\cdot 4-5\cdot 9=-37.$$

   Теперь поменяем местами первую и вторую строки. Получим определитель $\left| \begin{array} {cc} 9 & 4 \\ 2 & 5 \end{array} \right|$. Вычислим полученный определитель: $\left| \begin{array} {cc} 9 & 4 \\ 2 & 5 \end{array} \right|=9\cdot 5-4\cdot 2=37$. Итак, значение исходного определителя равнялось (-37), а у определителя с изменённым порядком строк значение равно $-(-37)=37$. Знак определителя изменился на противоположный.

3. Определитель, у которого все элементы строки (столбца) равны нулю, равен нулю.

   Пример применения этого свойства: показать\скрыть

   Так как в определителе $\left| \begin{array} {ccc} -7 & 10 & 0\\ -9 & 21 & 0\\ 2 & -3 & 0 \end{array} \right|$ все элементы третьего столбца равны нулю, то определитель равен нулю, т.е. $\left| \begin{array} {ccc} -7 & 10 & 0\\ -9 & 21 & 0\\ 2 & -3 & 0 \end{array} \right|=0$.

4. Определитель, у которого все элементы некоей строки (столбца) равны соответствующим элементам иной строки (столбца) равен нулю.

   Пример применения этого свойства: показать\скрыть

   Так как в определителе $\left| \begin{array} {ccc} -7 & 10 & 0\\ -7 & 10 & 0\\ 2 & -3 & 18 \end{array} \right|$ все элементы первой строки равны соответствующим элементам второй строки, то определитель равен нулю, т.е. $\left| \begin{array} {ccc} -7 & 10 & 0\\ -7 & 10 & 0\\ 2 & -3 & 18 \end{array} \right|=0$.

5. Если в определителе все элементы одной строки (столбца) пропорциональны соответствующим элементам иной строки (столбца), то такой определитель равен нулю.

   Пример применения этого свойства: показать\скрыть

   Так как в определителе $\left| \begin{array} {ccc} -7 & 10 & 28\\ 5 & -3 & 0\\ -15 & 9 & 0 \end{array} \right|$ вторая и третья строки пропорциональны, т.е. $r_3=-3\cdot{r_2}$, то определитель равен нулю, т.е. $\left| \begin{array} {ccc} -7 & 10 & 28\\ 5 & -3 & 0\\ -15 & 9 & 0 \end{array} \right|=0$.

6. Если все элементы строки (столбца) имеют общий множитель, то этот множитель можно вынести за знак определителя.

   Пример применения этого свойства: показать\скрыть

   Рассмотрим определитель $\left| \begin{array} {cc} -7 & 10 \\ -9 & 21 \end{array} \right|$. Заметьте, что все элементы второй строки делятся на 3:

   $$\left| \begin{array} {cc} -7 & 10 \\ -9 & 21 \end{array} \right|=\left| \begin{array} {cc} -7 & 10 \\ 3\cdot(-3) & 3\cdot 7 \end{array} \right|$$

   Число 3 и есть общий множитель всех элементов второй строки. Вынесем тройку за знак определителя:

   $$ \left| \begin{array} {cc} -7 & 10 \\ -9 & 21 \end{array} \right|=\left| \begin{array} {cc} -7 & 10 \\ 3\cdot(-3) & 3\cdot 7 \end{array} \right|= 3\cdot \left| \begin{array} {cc} -7 & 10 \\ -3 & 7 \end{array} \right| $$

7. Определитель не изменится, если ко всем элементам некоей строки (столбца) прибавить соответствующие элементы иной строки (столбца), умноженные на произвольное число.

   Пример применения этого свойства: показать\скрыть

   Рассмотрим определитель $\left| \begin{array} {ccc} -7 & 10 & 0\\ -9 & 21 & 4 \\ 2 & -3 & 1 \end{array} \right|$. Прибавим к элементам второй строки соответствующие элементы третьей строки, умноженные на 5. Записывают это действие так: $r_2+5\cdot{r_3}$. Вторая строка будет изменена, остальные строки останутся без изменений.

   $$ \left| \begin{array} {ccc} -7 & 10 & 0\\ -9 & 21 & 4 \\ 2 & -3 & 1 \end{array} \right| \begin{array} {l} \phantom{0}\\ r_2+5\cdot{r_3}\\ \phantom{0} \end{array}= \left| \begin{array} {ccc} -7 & 10 & 0\\ -9+5\cdot 2 & 21+5\cdot (-3) & 4+5\cdot 1 \\ 2 & -3 & 1 \end{array} \right|= \left| \begin{array} {ccc} -7 & 10 & 0\\ 1 & 6 & 9 \\ 2 & -3 & 1 \end{array} \right|. $$

8. Если в определителе некая строка (столбец) есть линейная комбинация иных строк (столбцов), то определитель равен нулю.

   Пример применения этого свойства: показать\скрыть

   Сразу поясню, что означает словосочетание "линейная комбинация". Пусть у нас есть s строк (или столбцов): $A_1$, $A_2$,..., $A_s$. Выражение

   $$ k_1\cdot A_1+k_2\cdot A_2+\ldots+k_s\cdot A_s, $$

   где $k_i\in R$ называется линейной комбинацией строк (столбцов) $A_1$, $A_2$,..., $A_s$.

   Для примера рассмотрим такой определитель:

   $$ \left| \begin{array} {cccc} -1 & 2 & 3 & 0\\ -2 & -4 & -5 & 1\\ 5 & 0 & 7 & 10 \\ -13 & -8 & -16 & -7 \end{array} \right| $$

   В этом определителе четвертую строку можно выразить как линейную комбинацию первых трёх строк:

   $$ r_4=2\cdot{r_1}+3\cdot{r_2}-r_3 $$

   Следовательно, рассматриваемый определитель равен нулю.

9. Если каждый элемент некоей k-й строки (k-го столбца) определителя равен сумме двух слагаемых, то такой определитель равен сумме определителей, у первого из которых в k-й строке (k-м столбце) стоят первые слагаемые, а у второго определителя в k-й строке (k-м столбце) расположены вторые слагаемые. Иные элементы этих определителей одинаковы.

   Пример применения этого свойства: показать\скрыть

   Рассмотрим определитель $\left| \begin{array} {ccc} -7 & 10 & 0\\ -9 & 21 & 4 \\ 2 & -3 & 1 \end{array} \right|$. Запишем элементы второго столбца так: $\left| \begin{array} {ccc} -7 & 3+7 & 0\\ -9 & 21+0 & 4 \\ 2 & 5+(-8) & 1 \end{array} \right|$. Тогда такой определитель равен сумме двух определителей:

   $$ \left| \begin{array} {ccc} -7 & 10 & 0\\ -9 & 21 & 4 \\ 2 & -3 & 1 \end{array} \right|= \left| \begin{array} {ccc} -7 & 3+7 & 0\\ -9 & 21+0 & 4 \\ 2 & 5+(-8) & 1 \end{array} \right|= \left| \begin{array} {ccc} -7 & 3 & 0\\ -9 & 21 & 4 \\ 2 & 5 & 1 \end{array} \right|+ \left| \begin{array} {ccc} -7 & 7 & 0\\ -9 & 0 & 4 \\ 2 & -8 & 1 \end{array} \right| $$

10. Определитель произведения двух квадратных матриц одного порядка равен произведению определителей этих матриц, т.е. $\det(A\cdot B)=\det A\cdot \det B$. Из этого правила можно получить такую формулу: $\det \left(A^n \right)=\left(\det A \right)^n$.
11. Если матрица $A$ - невырожденная (т.е. её определитель не равен нулю), то $\det \left(A^{-1}\right)=\frac{1}{\det A}$.

Формулы для вычисления определителей

Для определителей второго и третьего порядков верны такие формулы:

\begin{equation} \Delta A=\left| \begin{array} {cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right|=a_{11}\cdot a_{22}-a_{12}\cdot a_{21} \end{equation} \begin{equation} \begin{aligned} & \Delta A=\left| \begin{array} {ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right|= a_{11}\cdot a_{22}\cdot a_{33}+a_{12}\cdot a_{23}\cdot a_{31}+a_{21}\cdot a_{32}\cdot a_{13}-\\ & -a_{13}\cdot a_{22}\cdot a_{31}-a_{12}\cdot a_{21}\cdot a_{33}-a_{23}\cdot a_{32}\cdot a_{11} \end{aligned} \end{equation}

Примеры применения формул (1) и (2) есть в теме "Формулы для вычисления определителей второго и третьего порядков. Примеры вычисления определителей" .

Определитель матрицы $A_{n\times n}$ можно разложить по i-й строке, используя следующую формулу:

\begin{equation}\Delta A=\sum\limits_{j=1}^{n}a_{ij}A_{ij}=a_{i1}A_{i1}+a_{i2}A_{i2}+\ldots+a_{in}A_{in} \end{equation}

Аналог данной формулы существует и для столбцов. Формула для разложения определителя по j-му столбцу выглядит следующим образом:

\begin{equation}\Delta A=\sum\limits_{i=1}^{n}a_{ij}A_{ij}=a_{1j}A_{1j}+a_{2j}A_{2j}+\ldots+a_{nj}A_{nj} \end{equation}

Правила, выраженные формулами (3) и (4), подробно проиллюстрированы примерами и пояснены в теме Понижение порядка определителя. Разложение определителя по строке (столбцу) .

Укажем еще одну формулу для вычисления определителей верхних треугольных и нижних треугольных матриц (пояснение этих терминов см. в теме "Матрицы. Виды матриц. Основные термины"). Определитель такой матрицы равен произведению элементов, стоящих на главной диагонали. Примеры:

\begin{aligned} &\left| \begin{array} {cccc} 2 & -2 & 9 & 1 \\ 0 & 9 & 8 & 0 \\ 0 & 0 & 4 & -7 \\ 0 & 0 & 0 & -6 \end{array} \right|= 2\cdot 9\cdot 4\cdot (-6)=-432.\\ &\left| \begin{array} {cccc} -3 & 0 & 0 & 0 \\ -5 & 0 & 0 & 0 \\ 8 & 2 & 1 & 0 \\ 5 & 4 & 0 & 10 \end{array} \right|= -3\cdot 0\cdot 1 \cdot 10=0. \end{aligned}

Основной числовой характеристикой квадратной матрицы является ее определитель. Рассмотрим квадратную матрицу второго порядка

Определителем или детерминантом второго порядка называется число, вычисленное по следующему правилу

Например,

Рассмотрим теперь квадратную матрицу третьего порядка

.

Определителем третьего порядка называется число, вычисленное по следующему правилу

В целях запоминания сочетания слагаемых, входящих в выражения для определения определителя третьего порядка обычно используют правило Саррюса: первое из трех слагаемых, входящих в правую часть со знаком плюс есть произведение элементов, стоящих на главной диагонали матрицы , а каждое из двух других – произведение элементов, лежащих на параллели к этой диагонали, и элемента из противоположного угла матрицы.

Последние три слагаемые, входящие со знаком минус определяются аналогичным образом, только относительно побочной диагонали.

Пример:

Основные свойства определителей матрицы

1. Величина определителя не изменяется при транспонировании матрицы.

2. При перестановки местами строк или столбцов матрицы, определитель меняет лишь знак, сохраняя абсолютную величину.

3. Определитель, содержащий пропорциональные строки или столбцы равен нулю.

4. Общий множитель элементов некоторой строки или столбца можно выносить за знак определителя.

5. Если все элементы некоторой строки или столбца равны нулю, то и сам определитель равен нулю.

6. Если к элементам отдельной строки или столбца определителя прибавить элементы другой строки или столбца, умноженные на произвольный невырожденный множитель , то величина определителя не изменится.

Минором матрицы называется определитель, полученный вычеркиванием из квадратной матрицы одинакового числа столбцов и строк.

Если все миноры порядка выше , которые можно составить из матрицы, равны нулю, а среди миноров порядка хотя бы один отличен от нуля, то число называется рангом этой матрицы.

Алгебраическим дополнением элемента определителя порядка будем называть его минор порядка, получаемый вычеркиванием соответствующей строки и столбца, на пересечении которых, стоит элемент , взятый со знаком плюс, если сумма индексов равна четному числу и со знаком минус в противном случае.

Таким образом

,

где соответствующий минор порядка.

Вычисление определителя матрицы путем разложения по элементам строки или столбца

Определитель матрицы равен сумме произведений элементов какой- либо строки (какого- либо столбца) матрицы на соответствующие алгебраические дополнения элементов этой строки (этого столбца). При вычислении определителя матрицы таким способом следует руководствоваться следующим правилом: выбирать строку или столбец с наибольшим числом нулевых элементов. Этот прием позволяет значительно сократить объем вычислений.

Пример: .

При вычислении данного определителя, воспользовались приемом разложения его по элементам первого столбца. Как видно из приведенной формулы нет необходимости вычислять последний из определителей второго порядка, т.к. он умножается на ноль.

Вычисление обратной матрицы

При решении матричных уравнений широко используют обратную матрицу. Она в известной степени заменяет операцию деления, которая в явном виде в алгебре матриц отсутствует.

Квадратные матрицы одинакового порядка, произведение которых дает единичную матрицу , называются взаимообратными или обратными. Обозначается обратная матрица и для нее справедливо

Вычислить обратную матрицу можно только для такой матрицы , для которой .

Классический алгоритм вычисления обратной матрицы

1. Записывают матрицу , транспонированную к матрице .

2. Заменяют каждый элемент матрицы определителем, полученным в результате вычеркивания строки и столбца, на пересечении которых расположен данный элемент.

3. Этот определитель сопровождают знаком плюс, если сумма индексов элемента четная, и знаком минус – в противном случае.

4. Делят полученную матрицу на определитель матрицы .

Похожие статьи